Damping and Resonance of Waves

Displacement –time and Displacement –distance graphs.

Wave motion occurs because of the vibration of particles from their resting position.

We can show the displacement of particle (from its rest position) at different times by plotting a DISPLACEMENT-TIME graph.

We can show the displacements of particles of the wave at a certain time by plotting a DISPLACEMENT-DISTANCE graph.


The relationship between speed, wavelength and frequency.

Frequency (f)= Velocity (v) / Wavelength (λ)
v = f x λ

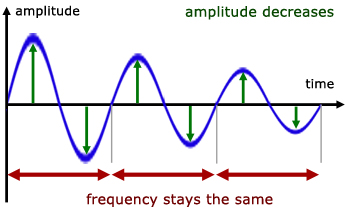
Damping in an oscillating system

Any motion that repeats itself in equal intervals of time is called a PERIODIC MOTION.

If a particle in a periodic motion moves back and forth over the same path, we call the motion OSCILLATORY or VIBRATORY.

Many of these oscillating bodies do not move back and forth between precise time fixed limits because frictional forces DISSIPATE the energy of the motion. Thus a pendulum stops swinging after some time.

The amplitude of oscillation of the simple pendulum will gradually decrease and become zero when the oscillation stops.

The decrease of in the amplitude of an oscillating system is called damping.

Two types of damping:
1. External damping: loss of energy to overcome frictional forces or air resistance.
2. Internal damping: loss of energy due to the extension and compression of the molecules in the system.

Damping in an oscillating system causes the amplitude and energy of the system to DECREASE but frequency DOES NOT change.

Source: http://www.a-levelphysicstutor.com/images/waves/reson-damp01.jpg

We CANNOT eliminate frictional force from the periodic motion of an object BUT we can cancel out its damping effect by feeding energy into the oscillating system so as to COMPENSATE for the energy dissipated by the frictional force.

For Example, the oscillating pendulum in a pendulum clock uses energy derived from the fall of a weight pulling a chain in the clock to supply external energy.

Resonance In An Oscillating System

When a system oscillates there is a loss of energy due to damping.
If the loss of energy is replaced by an external force of the same frequency, the system will continue to oscillate and may reach a bigger amplitude.

The external force supplies energy to a system, such a motion is called a forced oscillation.

Natural frequency is the frequency of a system which oscillates freely without the action of an external force.

RESONANCE occurs when a system is made to oscillate at a frequency EQUIVALENT at a frequency to its natural frequency by an external force. The resonating system oscillates at its MAXIMUM AMPLITUDE.

Here Resonance 1(R1) is more than Resonance 2 (R2)

The characteristics of resonance can be demonstrated with a Barton’s pendulum system.



Source: http://www.antonine-education.co.uk/Image_library/Physics_4/Further_Mechanics/Bartons_Pendula.JPG

You can read more about Barton's pendulum here:

http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=1598.0


Some effects of resonance observed in daily life:

The tuner in the radio or TV enables you to select programmes you are interested in .The circuit in the tuner is adjusted until resonance is achieved, at the frequency transmitted by a particular station selected. Hence a strong electrical signal produced.

The loudness of music produced by musical instruments such as the trumpet and flute is the result of resonance in the air.

The effect of resonance can also cause damage. For example, a bridge can collapse when the amplitude of its vibration increases as a result of resonance. aka when it vibrates at its natural frequency.