Half-life
Concept of Half-life
The reactivity or activity of a radioactive material is the rate of decay of the material.
The rate of decay is the same as the number of atoms which decay or are emmited every second.
The rate of decay of a radioactive materials depends on the number of atoms that have not yet undergone decay. Thus, the reactivity of a radioactive material will decrease with time.
The half-life (t½) of a radioactive element is the time taken for half the number of atoms in a sample of radioactive atoms to decay.
After one half-life, the activity and the number of atoms remaining of any radioactive substance are halved.
Decay curve.
The half-life of the same radioactive element is the same but the half-lives of different radioactive elements are different.
The value of half-life is not influenced by factors such as temperatures, pressure and etc.

(Source: bbc.co.uk)
Examples of half lives of some common isotopes
Radioisotope
|
Half-life
|
Uranium-238
|
5000 million years
|
Uranium-235
|
700 million years
|
Plutonium-239
|
24 000 years
|
Carbon-14
|
5700 years
|
Calcium-137
|
30 years
|
Cobalt-60
|
5 years
|
Determining the Half-life
Nuclei in a radioactive sample disintegrate at random.
Each nucleus has the equal chance of being decayed. Which means that at any time, any nuclei can decay / disintegrate.
Activity = the average number of decay or disintegrations per unit time in a radioactive sample.
During the decay of a radioactive sample, the number of atoms which have disintegrated increases, while the number of atoms which have not disintegrated decreases. It has to be remembered that the total number of atoms remain constant during this process.
The rate of decay lessens as the number of intact atoms that remain decreases and thus activity decreases with time as the number of undecayed atoms decreases.
It has to be noted that different radioactive elements decay at different rates.
Point: Half-life, t½ , of a radioactive isotope is the time taken for the activity of atoms of that isotope to fall to half of its original value.
also
Half-life (t½) can also be stated as the time taken for the number of radioactive atoms to decrease to half of its original number.
Consider this:
i. If N is the number of original atoms in a radioactive sample.
ii. After one half-life has lapsed, half (1/2)N atoms remain and half (1/2)N atoms have disintegrated.
iii. After two half-lives, (1/2)X(1/2)N = (1/2)^2 N = (1/4) N atoms remain and (3/4)N atoms have disintegrated.
*Remember: N - (1/4) N = (3/4) N
iv. This decay process continues until a stable atom is produced.
v. Say x = number of half lives
N = original number of atoms
Nx = number of atoms remaining after x half-lives, then we can say that
Nx = (1/2)^x N
(Remember the symbol ^ means to the power of)
Also, it is worth to consider these formulas:
An exponential decay process can be described by any of the following three equivalent formulas:
where
- N0 is the initial quantity of the substance that will decay (this quantity may be measured in grams, moles, number of atoms, etc.),
- N(t) is the quantity that still remains and has not yet decayed after a time t,
- t1/2 is the half-life of the decaying quantity,
- τ is a positive number called the mean lifetime of the decaying quantity,
- λ is a positive number called the decay constant of the decaying quantity.
The three parameters 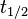 ,
,  , and λ are all directly related in the following way:
, and λ are all directly related in the following way:
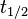 ,
,  , and λ are all directly related in the following way:
, and λ are all directly related in the following way:Source: wikipedia.com
Usage of Half-life
Half-life in Archeology
Carbon-14 has a half-life of 5600 years.
Humus, animals and plants absorb carbon-14 through carbon dioxide gas in the atmosphere. A small amount in CO2 exists as carbon-14.
Living animals and vegetable have a constant amount of Carbon-14 because the c-14 decayed will always replaced.
However or dead beings the amount of C-14 in it will decrease because new C-14 will not be absorbed causing its reactivity to decrease.
When an antique or human skill are found, their age can be determined by
Measuring the reactivity of C-14 in it.
Determine the ratio of decay carbon-14 against intact carbon-14.
Industries:
Radioisotopes can be used as tracers, in order for it to be feasible, the radioisotopes used must have long enough half-lives. For example: the leaks in undergound pipes carrying oil can be detected by injecting radioactive tracer into the flow. Afterwards a GM tube can be utilised to sense the leakage from the surface above the pipe.
Medicine:
To be useful in the medical field, the radioisotope must have a short half-life. This is to prevent over exposure to radiation for an unnecessarily long period of time.
The isotope Iron, 59Fe with a half life of 45 days is used in testing for iron in blood plasma.
Iodine, 131 I with a half life of 8 days can be used in thyroid tests and treatments.




2 comments:
thanks!
Do you have notes for the operations of nuclear radiation detectors?
Post a Comment